The Tree Container Library

This bit of code (click on the code link to the right) shows the sequential_tree container at work. It uses functions to perform many of the same operations performed in the generic example. The code illustrates how the sequential_tree container is used. The code can be viewed an printed from the icon to the right.
A source file of this example can be downloaded here.
This example is compatible with versions 3.50 and higher of the TCL. The latest version of the TCL can be downloaded from the TCL download page.

This generic example, as well as the library, is compatible with Visual C++ 6.0, 7.0, and 8.0, as well as GCC. For the VC6 compiler, users need to un-check the Enable minimal rebuild option for successful compilation. Also for VC 6.0 users, the normal #pragma warning (disable : xxxx) directive is necessary to avoid the compiler warnings.

The #include in line 1 is commented out. Microsoft compilers need this line, so if you're compiling with a microsoft compiler, you can un-comment this line. Line 2 includes the header for sequential_tree. Since we will be working with the sequential_tree container exclusively, we won't need to include the header for the other trees. Lines 3 - 5 include STL needed headers.

Line 7 declares a namespace utility, where we will define our utility functions. Line 9 declares the load_tree() function. This function is very similar the function of the same name in the generic example. Line 10 declares the function traverse_tree(), and line 11 starts the definition of traverse_tree(). Both of these functions are the same as described in the generic example, and will not be described here. The same is true of the function is_last_child() beginning on line 33.

Lines 42 - 56 define the class CAlpha, which will be our stored_type. Notice that a less-than operator has been defined for this class. This definition is not required for the sequential_tree, because sequential_tree uses a std::vector for it's internal storage, rather than a std::set, which is used by the associative trees. It is required, however, to be able to call sequential_tree's sort() (parameter-less) function, as we do in this example. sequential_tree's sort() (with no parameter) function uses the less-than operation of stored_type, to sort the child nodes within a parent node.

Lines 58 - 61 define a predicate function which will be used for one of the methods to sort sequential_tree's child nodes. Notice that it performs the comparison lhs.get_text() > rhs.get_text() which has the affect of sorting child nodes in descending order. Lines 63 - 69 define a function object which will also be used for one of the methods to sort the child nodes. Notice that it performs the comparison lhs.get_text() > rhs.get_text() which has the affect of sorting child nodes in descending order.

Lines 71 - 100 define main(). Line 74 declares the sequential_tree object we will use in this example, and sets it's root node. Line 76 calls a utility functions which loads the tree. Line 77 calls a utility function which prints the tree. The function print_tree() is the same function as described in the generic example. Line 80 sorts only the child nodes within the root node, using the less-than operator defined in CAlpha, which will sort the nodes in an ascending manner. Note that the sort() functions sort only the children within the node which the function is called, while the sort_descendant() operations sort the descendants within the node which the function is called. Line 81 sends a description of the tree to std::cout, and line 82 prints the tree structure.

Line 85 sorts all the descendants of the root node, which is the whole tree structure. Since sort_descendant() is called with no parameters, the less-than operator of CAlpha determines the sort order, which is ascending. Lines 86 - 88 display the newly sorted tree structure. Line 90 sorts the children only, within the root node, using the binary predicate function defined on line 58. This predicate function is defined to sort the nodes in a descending manner, so the operation will sort the root nodes children (nodes A, B & C) in a descending order. Lines 91 - 93 display the newly sorted tree structure.

Line 95 sorts all the descendants of the root node (the whole tree), using the function object defined on line 63. The function object is defined to sort the nodes in a descending order also, so after performing this operation, all the nodes in the tree structure will be ordered in a descending order. Lines 96 - 98 display the newly sorted tree structure.

Line 100 calls a function which demonstrate the use of descendant iterators. This function is described in detail in the generic example.

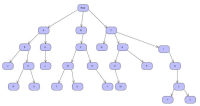
Line 106 begins the function which loads (inserts) the tree nodes. Line 109 creates a tree iterator. This iterator is created in the same manner as all the trees in the TCL. Line 112 inserts the first node, A, into the root node. If insert() is used with only a single parameter specifying the node to be inserted, that node is inserted as the last child within the node. Another insert() operation, described below, accepts an additional (first) parameter, which specifies the position in which to insert the new child node. Line 113 insures the node was inserted successfully. Since it now points to node A, lines 118 and 119 can use this iterator to insert nodes E and D into node A. Note the order in which nodes E and D are inserted. sequential_tree, unlike the associative trees does not naturally order child nodes within their parent, so the nodes will be ordered in the way they are inserted, until a sort() operation is performed on the parent node.

Line 121 positions it at node E, and line 122 moves it to node D. Line 124 inserts node J into node D. Line 126 inserts node K into node D, storing an iterator to the newly inserted node. Then, nodes S and R are inserted into node K in lines 129 and 130. Line 133 decrements it back to node E, where line 135 inserts node L.

Line 137 inserts node B in the root node, and line 138 inserts node F in node B. Line 141 shows that the TCL iterators can be assigned. Line 142 inserts node M into node F, and lines 144 and 145 insert nodes T and U into node M. Line 148 inserts node N into node F, and line 150 inserts node V into node N.

Line 152 positions it at the first child of the root node, or node A. Line 153 increments it to point to node B. Line 154 demonstrates another form of sequential_tree's insert(). The first parameter of this insert() operation specifies the position at which the new node will be inserted. The new node given as the second parameter will be inserted immediately before the iterator specified as the first parameter. In this case, node C will be inserted before node B. Lines 156 and 157 insert nodes G and H into node C, and line 160 inserts node O into node H.

Line 162 position it at node O, and lines 165 inserts node W into node O. Node P is then inserted into node H in line 167. Line 170 demonstrates the use of the parent() operation. At this time, it points to node H, so the parent() operation returns node C which is used to insert node I (into node C). Line 171 makes it point to node I, and lines 174 inserts node Q into node I. Line 177 inserts node X into node Q, and line 179 inserts node Z into node X. Line 180 also inserts node Y into node X, and since it uses the two parameter form of insert, and the first parameter points to the first child, node Y is inserted before node Z.

By studying the output from the program, you can validate the operations of the insertions, iterations, and sort behavior.