The Tree Container Library

This bit of code (click on the code link in figure 1) shows all three associative trees containers at work. Since this example makes use of the find() operation, which is only available to the associative_trees, the sequential_tree is not included in this example. The example uses template functions to perform the same operations on the three different tree types. The code illustrates the differences between the tree containers. The code can be viewed an printed from the icon to the right.
A source file of this example can be downloaded here.
This example is compatible with versions 3.50 and higher of the TCL. The latest version of the TCL can be downloaded from the TCL download page.

This generic example, as well as the library, is now compatible with Visual C++ 6.0, VC7, VC8, and gcc. For the VC6 compiler, users need to un-check the Enable minimal rebuild option for successful compilation. Also for VC 6.0 users, the normal #pragma warning (disable : xxxx) directive is necessary to avoid the compiler warnings.

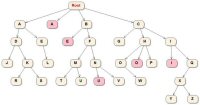
The letters A to Z are inserted in the tree's to form the tree structure (shown to the right). The tree structure shows duplicated nodes for the vowels in a different color. Depending on the tree container, not all of these duplicate nodes will appear in all the containers. A sample of the results to the console is also given to the right.

Line 1 is used for Visual Studio compilers. Those using MS compilers can un-comment this line.
Lines 2 - 4 include the three types of tree containers from the TCL. If you have the TCL placed in a separate directory, you may need to modify the paths on these lines.

Lines 9 - 42 declare and in two cases, define the utility functions, placed in a namespace for convenience. The functions are templatized, to accept all three types of tree containers.

Lines 11 and 12 declare a function which will be covered further below. Line 14 begins a template function which prints the tree structure to std out, using simple recursion. Line 16 prints the name of the current node. Line 18 declares a const_iterator to iterate over the child nodes. Lines 19 - 32 iterate over the children within a given parent. The loop in lines 20 - 28 are needed only to print the lines connecting the nodes, and to determine the amount of indent for a given child node. To do this, the parent nodes are obtained repeatingly to the current depth, to determine if the parent in question is the last child. If so, the vertical lines moving down from the nodes are not displayed. Line 181 prints the vertical line under the parent node at the current depth. Line 182 prints the small horizontal line before the node. Line 31 calls itself recursively.

The function starting on line 35 is needed to determine if the passed node is the last node within it's parent. It does this by obtaining the pointer to it's parent, in line 37. Then an iterator to the last node in the parent is obtained in lines 38 - 39. This is safe, because we know the parent contains at least one node, (the node which was passed). Line 40 compares the passed node against the last node of the parent, and returns the result.

Lines 44 - 58 define a class, CAlpha, which will serve as the storage type for the trees, to store in the tree nodes. It's a very basic class, which only holds the state of name that it's given. As with the STL, a default constructor must be present to use the class in the TCL. Also, notice that the less operator is defined. If this operator isn't defined for the storage class, a comparison operation must be supplied explicitly as the second template parameter in the tree declarations. Also, a constructor accepting a string is supplied for convenience.

Line 60 starts main().
Lines 62 - 68 load, print, and traverse the sample tree container.
Lines 70 - 76 load, print, and traverse the sample multitree container.
Lines 78 - 84 load, print, and traverse the sample unique_tree container.
Lines 63, 71, and 79 declare the tree containers. The container declarations are very similar to that of the STL containers. The second template parameter is not needed in the declarations, since CAlpha defines it's own < operator. The second template parameter for all three tree containers defaults to std::less<stored_type>, where CAlpha is stored_type in this case, which causes the < operator or CAlpha to be used for the node comparisons.
The tree constructors take an argument of stored_type. This allows the constructors to set the root node element and it's text. This text will be used in the output, when the tree's are printed to std::cout.

Line 89 begins the template function which populate the tree containers. The template parameter, T, parametizes the type of container passed, or, in succession:
tree<CAlpha>, multitree<CAlpha>, and unique_tree<CAlpha>
Line 92 creates a child iterator. This iterator will be used for finding, traversing, and inserting nodes.
Beginning with version 3.50 of the TCL, the * and -> operations of the iterators return a reference and pointer to the element contained in the nodes, not to the nodes themselves, as in previous versions. Thus, to access the underlying node from an iterator, we must use the iterator's node() operation. Line 95 inserts the first node into the tree. Notice that the insert() operation takes a stored_type, (an object of the type being stored), or in this case, a CAlpha object. Notice also that the insert() operation returns an iterator. This iterator will point to the inserted node if successful, or to the end() iterator of the parent, if unsuccessful. Line 96 tests that the insertion was successful. Tree const_iterators, like the const_iterators in the STL, can only access stored_type's (CAlpha) const class members.

Line 98 attempts to insert a duplicate node in the root node. A duplicate node is determined by the comparison operation of the tree, in this case, the < operator of CAlpha. This insert() operation will fail for the tree container, since duplicate nodes are not allowed under a given parent. It will also fail for the unique_tree container, since duplicate nodes are not allowed in the entire tree, let alone a given parent. The operation will be successful in the multitree container, since duplicate nodes are allowed under a given parent in the multitree container.
Lines 99 - 100 test the outcome of the duplicate insertion, and display the results to std::cout.

Line 103 positions the iterator at the beginning node of the tree, or node A. The begin() operation returns an iterator to the first node of a node (not necessarily the root) that it's called on. If the node contains no children, then the node's end() iterator is returned. Remember that a tree is regarded as an ordinary node, and that all nodes in a tree can be considered trees themselves.
Line 105 inserts node D in node A. Notice that the insertion operation is performed on the iterator through the iterator's node() operation. This shows how the underlying node operations are exposed to the iterator with the iterator's node() operation. A second iterator is created, child_it, and used for the remaining of the function, to retreive the return iterator value of insert operations performed by the first created iterator. Line 106 inserts node E also in node A. Since no nodes will be inserted in node E, the return iterator of the insert() operation need not be saved.

Line 109 shows that you can assign one iterator to another. Line 111 inserts node J in node D. Since no nodes will be inserted in node J, the return iterator need not be saved. Node K is then also inserted in node D in line 113. The return iterator is saved, since nodes will be inserted in node K. Nodes R and S are inserted in node K in lines 116 - 117. At this time, iterator it points to node D. After incrementing it in line 120, it will point to node E. Line 122 then inserts node L in node E.

With all the descendents of node A, line 124 inserts node B in the root node. Then an attempt is made in line 126 to insert a second node E in node B. Since this second node E has a different parent than the first node E, the insertion will succeed for tree, as well as for multitree. It will fail for unique_tree, however, since unique_tree guarantees that every node in the entire tree will be unique. Lines 127 - 128 display the results of the insertion of the second node E.

In line 129, node F is next inserted in node B. Then in line 132, Node M is inserted in node F. In lines 134 - 135, nodes T and U are inserted in node M. Since iterator it still points to node F, it is used in line 138 to insert node N in node F. Line 140 makes an attempt to insert a second node U. Since the second node U has a different parent than the first node U, the insertion will be successful for tree and multitree. It will fail, however for unique_tree. Line 140 tests for the success of the insert operation be testing the return value of insert() directly. Line 141 displays the results of the insert operation if unsuccessful. Line 143 inserts node V into node N.

With the descendants of node B inserted, line 145 inserts node C in the root node. Nodes G and H are inserted in node C in lines 147 - 148. Node O is then inserted in node H in line 151. In line 153, an attempt is made to insert a second node O in node H. This insertion should fail for tree, since tree insures all nodes are unique with a given parent. The insertion will also fail for unique_tree.

Since iterator it now points to node H, and the first insertion of node O in node H was successful, line 157 will set child_it to node O. Line 160 then inserts node W in node O. With iterator it still pointing to node H, line 162 inserts node P in node H.

Line 165 inserts a node using the parent() operation. Since iterator it now points to node H, and node H's parent is node C, line 165 inserts node I in node C. Afterwards, in line 169, an attempt is made to insert another node I, in the first node I. Of course, the operation will be successful for multitree. Since the two node I's have different parents, the insertion will also be successful for tree. The insertion will fail for unique_tree. Lines 170 - 171 display the result of the failed insertion.

With iterator it pointing to the first node I, line 174 inserts node Q in node I. Line 177 then inserts node X in node Q. And finally, lines 179 - 180 insert nodes Y and Z in node X.

The function template starting on line 185 uses the descendant iterators (see here) to traverse all three trees in pre-order, post-order, and level-order manners. A list of nodes is printed for each type of descendant iterator to check the behavior of the iterators. Lines 189, 196, and 203 print the tree type and descendant iterator type. Lines 190, 197, and 204 declare the descendant iterators. Notice that a non-const descendant iterator is created for the pre_order_iterator, while const descendant iterators are created for the post_order_iterator and level_order_iterator. In this example, it doesn't matter if the iterator is const or non-const, because the operations performed on the iterators are const operations. If non-const operations were being performed on the iterators, all of them would need to be non-const.

Lines 191, 198, and 205 start the iterators looping through the tree structures. The syntax of the descendant iterator use is very similar to that of the STL iterators. Lines 192, 199 and 206 print the text of the current node.